前言
一道leetcode上的题目:
给定一个整数数组 nums,将数组中的元素向右轮转 k 个位置,其中 k 是非负数。
初级算法 - LeetBook - 力扣(LeetCode)全球极客挚爱的技术成长平台
示例 :
输入: nums =,
输出:
解释:
向右轮转 1 步:
向右轮转 2 步:
向右轮转 3 步:
显而易见这是一种轮换,但可能是多次轮换,它不改变数组本身,只改变元素的位置。也就是说,这是一个置换。
先回忆下一个置换的写法:
设是n元集合上的一个双射置换,为了简单记为。令表示上的一个置换,第一行表示原象,第二行表示像的集合。
我们可以写出示例中的置换群表示:
也就是把1号位的换成5号位的,把2号位的换成6号位的,3号位的换成7号位的,依此类推。
这个置换是直观的,也是容易理解的,我们很容易就有了第一种想法。
算法尝试
置换表示
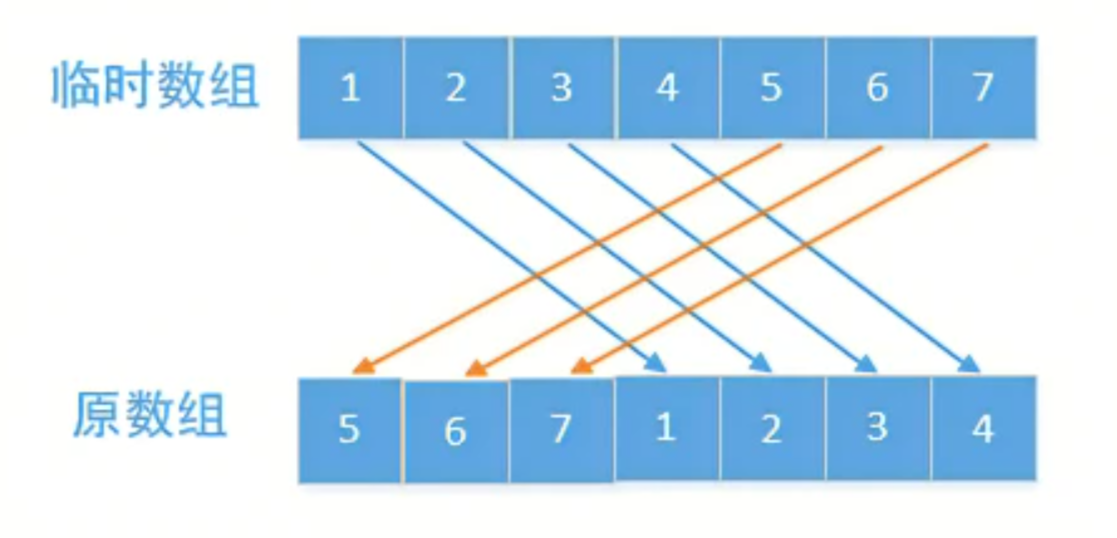
置换是非常直观的方法,但问题是,如果我直接把1号位的元素换成5号位的,那我就必须将1号位的元素放在一个临时变量里,否则直接赋值的话,1号位的元素就被覆盖了。
我们可以使用一个临时数组,先把原数组的值存放到一个临时数组中,然后再把临时数组的值重新赋给原数组,重新赋值的时候要保证每个元素都要往后移k位,如果超过数组的长度就从头开始,所以这里可以使用(i + k) % length来计算重新赋值的元素下标。
public void rotate(int nums[], int k) {
int length = nums.length;
int temp[] = new int[length];
//把原数组值放到一个临时数组中,
for (int i = 0; i < length; i++) {
temp[i] = nums[i];
}
//然后在把临时数组的值重新放到原数组,并且往右移动k位
for (int i = 0; i < length; i++) {
nums[(i + k) % length] = temp[i];
}
}
轮换表示
相信不用我说都看出来了,如果这个数组特别大的时候,这样做的内存消耗是很大的。
但是众所周知,一般的置换表示可以写成轮换表示。
定义:一个置换如果把数码变成,变成,…,变成,又变成,而使得其余的元(假如还有的话)都不变,则称为一个k-轮换(循环)置换。记为:
注:2-轮换简称为对换。恒等映射通常记为(1)
我们把上文示例的置换表示改写成轮换:
实际上,有定理保证,对于每个置换都可以写成若干个不相连的轮换之积,因此这种写法总是可行的。
我们观察轮换元的规律,似乎是将数组视作一个环形,1号位向右移3位到达4号位,4号位向右移3位到达7号位,7号位向右移3位到达10号位,由于最后一个与第一个相连,因此8号位就是1号位,10号位就是3号位。
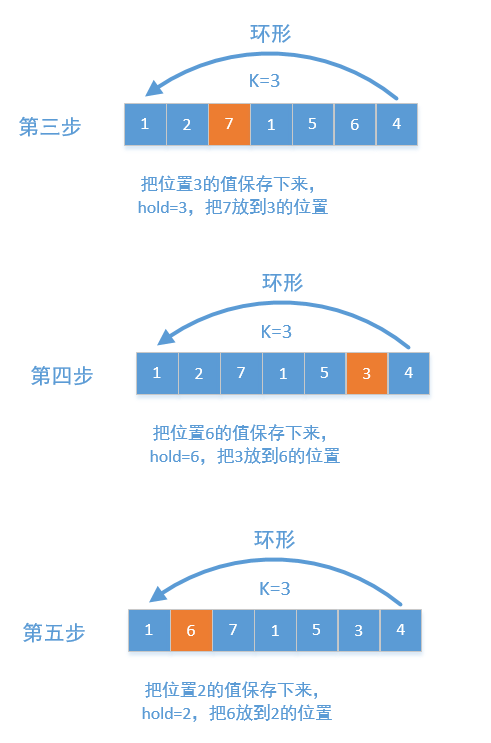
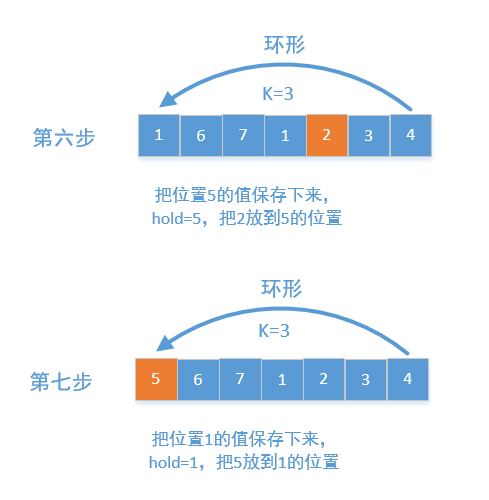
依照这个思路,我们可以写出轮换表示的算法。
public static void rotate(int[] nums, int k) {
int hold = nums[0];
int index = 0;
int length = nums.length;
boolean[] visited = new boolean[length];
for (int i = 0; i < length; i++) {
index = (index + k) % length;
if (visited[index]) {
//如果访问过,再次访问的话,会出现原地打转的现象,
//不能再访问当前元素了,我们直接从他的下一个元素开始
index = (index + 1) % length;
hold = nums[index];
i--;
} else {
//把当前值保存在下一个位置,保存之前要把下一个位置的
//值给记录下来
visited[index] = true;
int temp = nums[index];
nums[index] = hold;
hold = temp;
}
}
}这里需要注意的是,如果数组长度length和轮换步长k不互质的话,将会在某一次轮换后回到原点。因此保留了一个数组visited表示这个元素有没有被访问过,如果被访问过就从他的下一个开始,防止原地打转。
此时意味着该置换群不止一个不相连轮换。
对换表示
我们还是希望在轮换的基础上更进一步。一般的置换方法中,我们需要有一个大的临时数组,一般来说会带来很大的内存消耗。轮换方法中,数组的下标需要依赖大量的求余运算,这种运算总是更耗时的。
如果我们可以找到一个简单的方法,通过对换就能实现算法,那应该既能避免大的内存消耗,也能够节省时间。我们来看看chatGPT和leetcode给的答案。
public void rotate(int[] nums, int k) {
int length = nums.length;
k %= length;
reverse(nums, 0, length - 1);//先反转全部的元素
reverse(nums, 0, k - 1);//在反转前k个元素
reverse(nums, k, length - 1);//接着反转剩余的
}
//把数组中从[start,end]之间的元素两两交换,也就是反转
public void reverse(int[] nums, int start, int end) {
while (start < end) {
int temp = nums[start];
nums[start++] = nums[end];
nums[end--] = temp;
}
}leetcode和chatGPT给出的答案都是利用翻转实现的。
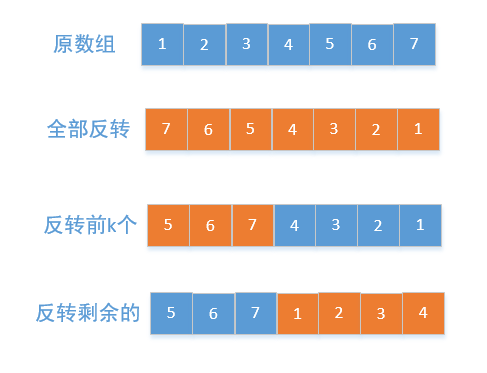
当然,大家都知道,反转无非就是一前一后的数组元素进行对换。也就是说反转给出的算法其实正是对换操作。
对换与轮换
显而易见地,对换方法在时间上有着得天独厚的优势。但我们在这里讨论一点更数学的问题。
假如我们采用翻转的方法去实现功能,我们需要对数组元素进行对换操作。我想谈论的问题是:
1、翻转方法中,至多几次对换操作,就能够保证对所有情况都能达到预期效果。
答案:次。(为数组长度)
2、至少几次对换操作,才能够保证对所有情况都能达到预期效果。
答案:次。(为数组长度)
(第二问的意思是,如果你只能进行次对换操作,那么无论你怎样优化算法,总有数组你无法达到预期效果)
第一问的答案是容易证明的。
证明:共进行了三次翻转,第一次对数组个元素进行翻转,第二次对数组前个元素进行翻转,第三次对数组后个元素进行翻转。
容易证明对i个元素的数组进行翻转需要次对换,则总共需要次对换
注意到,因此,不可能同时为奇数,也不可能只有两个偶数,因此只有两种情况,两奇一偶,三偶。
三者都为偶数时,取整号可以直接拆掉,此时共次对换。
两个为奇数,一个为偶数时,可将其改写成,且此时,此时共次对换。
因此至多次对换。
第二问需要借助两个置换群的定理。
定理1:任何一个轮换都可以表示为若干个对换的乘积,且对换数等于。比如:
按从右向左的运算原则,显然有:
其他,保持不变,因此定理1成立。
定理2:将一个置换分解为不相交轮换的乘积,如果不考虑因子的次序和乘积中1轮换的个数,则这个分解式是唯一的。
可以将每一个轮换都看作一个圆,这个圆和其他圆不相交,这个圆上的点做任何拓扑上的改变都会导致置换的结果发生变化,因此置换的分解公式是唯一的。
定理3:每个置换都可以表示为对换的乘积。
根据定理2,每个置换分解为唯一的不相交轮换的乘积,每个轮换可以分解为对换的乘积。因此每个置换都可以表示为对换的乘积。
下面我们就可以开始证明了:
以下证明默认
证明:我们首先需要证明,对于题目中的全轮换,当时,其置换群的轮换表示必定包含到。
其实就是证明不存在数组某一元素位置没有发生改变,全轮换后,数组下标(假设由1开始)将会变成。因此轮换表示必定包含所有元素。
先将置换分解为不相交轮换的乘积,设不相交轮换数为,又定理1可知,一个轮换可以拆成个对换,因此总共有个对换。
由于置换至少可以分解成一个不相交轮换,因此至少次对换操作,才能够保证对所有情况都能达到预期效果。
我们可以根据这个思路,将置换群转换为若干个对换的乘积,原则上说,是比翻转算法至少少一次对换。
当然,如果我们先写出置换群,在分解成轮换群,最后再分解成对换的乘积,这显然是不够效率的,所幸这题是一个全轮换群,全轮换群的乘积是非常容易计算的。
以下同样默认,则其中一个不相连轮换群乘积可表示成:
其中,
我们在进行数组索引的时候,是从开始的,因此,实际写代码的时候也不需要这个恼人的了。
public void rotate(int[] nums, int k){
k = k% nums.length;
if(k!=0){
Overlay(nums,k);
}
}
public void Overlay(int[] nums,int k){
int length = nums.length;
int index1=0;
int index2=k;
int group_amount=1;//群元数
int total_length=0;//群元长度
for(int i=0;i<length & total_length<length;i++){
total_length++;
index1=length-i-1;
index2=(index1+length-k)%length;
for(int j=0;j<length-1;j++){
if(index2==length-i-1){
group_amount++;
break;
}
exchange(nums,index1,index2);
index1=index2;
index2=(index2-k+length)%length;
total_length++;
}
}
}
public void exchange(int[] nums,int i,int j){
int temp=nums[j];
nums[j]=nums[i];
nums[i]=temp;
}我们唯一需要注意的也许是实际对换操作的时候,我们是右结合,因此是倒着生成对换群,倒着对换的。
数组最后一个元素的指标是,因此我们还是看到了这个恼人的。
这其实类似第二种方法,唯一不同的是,第二种方法通过visited数组避免重复索引,在这里,其实就是置换群分解成了多个不相连的轮换群,而我们只在其中一个轮换群中进行轮换。这里的方法是通过索引数组角标,当回到原点的时候,跳出循环。
好吧,是个负优化。还是跟第二个方法问题一样,索引脚标的时候出现了大量的求余计算。我们为了那一次的对换提升,花费了大量的运算。
但反过来说,我们从某种程度上证明了,如果我们只通过对换解决这个问题,那么翻转算法速度上就是最优解。因为它至多用了次对换,而理论上限是,但次对换的算法需要大量求余。
对换与翻转
我们刚才说过翻转算法需要或次对换,而轮换分解则需要次对换。
很自然我就有一些疑问,这个能不能被事先求出来,他们的对应关系是怎么样的。
要解答这两个问题首先需要证明在第二个方法中提到的一句话:
如果数组长度length和轮换步长k不互质的话,将会在某一次轮换后回到原点。
事实上这句话的关键在于,如果数组长度length和轮换步长k不互质,那么至少存在两个或以上的不相连轮换群。
以下证明默认
证明:首先根据轮换群乘法,本问题中可能出现的置换群的一个不相连轮换群可表示成:
有
这是自然的,因为对于该轮换群,其对换过程为
如果与互质,则当且仅当时成立,此时该不相连轮换群长度为,已经包含了所有元素。数组中找不出与它不公共的元素,因此它是唯一的不相连轮换群。
因此当与不互质时,至少存在两个或以上的不相连轮换群。
通过以上的证明我们能感受到,当时,有几个满足,置换群就能分解成几个不相连轮换群的乘积。
但是大家会注意到如果,那么同样满足,一直往上,并且一定满足。因此应该是和的最小公倍数。此时,,一共有个。
翻转算法到底需要次还是次对换,取决于他们的奇偶分布,轮换分解则需要次对换,与和的最小公倍数有关,因此两者并不能直接建立起联系。
但是他们还是有点关系的,参考下面的定理。
定理4:虽然一个置换表示成对换的个数不唯一,但所用对换个数的奇偶性是唯一的。
翻转算法需要次对换时,和都必须是偶数,此时和不互质,因此存在两个或以上的不相连轮换群,所以必须也会偶数。这样,和就都是偶数了。次的情况同理。



