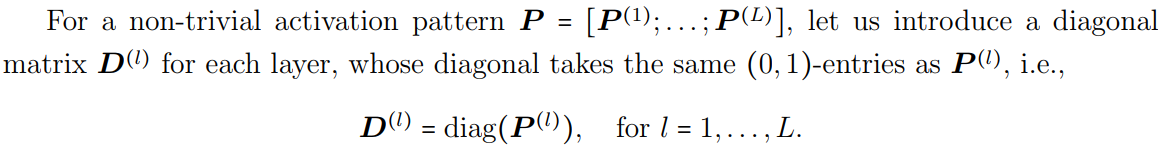论文链接
论文简介
这篇文章是一篇偏神经网络理论的文章,指出任何的深度网络都可以重写成一个功能相同的的三层网络,与万能逼近定理不一样的是,这个构造是无误差的,他们是完全等价的。
整体思路
在正式介绍之前,需要简单介绍一下前人的工作,总的来说就是一句话:网络可以表示为局部线性模型的集合,简单地说网络就是一个很多个区域的分段函数,每个区域的函数都是线性函数。
例如,一个网络可以表示成这样:
(如果没有特别说明,后续的均视作输入向量)
首先,我们将解空间分割为三个区域,对应的函数分别是。接着,我们对这里进行一点点的改写
我们改写成这样的原因是,这是函数的线性组合,我们可以写成一个向量点积的形式:
我们不妨把前面的系数向量称作选择向量,毕竟它将我们希望的函数给挑选出来了。
好吧,但我们还是很讨厌分段函数,如果说,我们能找到一个函数,他能根据所在的区域,给出我们所希望的选择向量,那么我们将能得到一个非常紧凑的形式:
而这就是这篇论文等价表述的思想,用矩阵描述代替分段函数。
但这里有两个问题很关键,首先,我们能否精准表示出。
在论文中,作者给出了前人的工作,在“ReLU Deep Neural Networks from the Hierarchical Basis Perspective”文章中,证明了实空间紧致子空间上的每一个分段线性函数都可以用一个深度和宽度都有限的神经网络精确表示。
其次,如果要根据所在的区域,给出我们所希望的选择向量,那么我们就需要有一套有效的描述区域的手段。
作者也给出了相应的内容,在“Unwrapping the black box of deep relu networks: interpretability, diagnostics, and simplification”中,有提到对于每一个区域,都是一个多胞体,它可以被定义为有限个线性不等式的结集,即有限个半平面的交集。因此我们可以通过描述半空间,来判断所在的区域。
数学推导
第一个构造
一个多胞体可以由一组半空间指定整个分区。特别地,我们令是声明所有分区的最小半空间集合,其中是一条描述半空间的不等式。
或者改写成我们一会见得更多的形式:
换句话说,所有分区都可以写成中某几个半空间的交集。
我们先找到一个矩阵能够储存所有的超平面方程:
或者写成一个:
数学上一般将这个式子称为超平面。
这样,矩阵方程每一行都唯一描述了一个超平面方程。
我们现在假设空间上有一个点,它所在的空间恰好可以由三个半空间交集而成。
这意味着他将同时满足下面三条不等式:
这也意味着第一、二、五行都是小于的。(可能会有其他行也是小于的,但描述这个点并不需要那部分的半空间条件)
由于第一、二、五行都是小于的,因此第一、二、五行都是等于的。
到这一步,我们至少把所在的半空间条件给挑出来了。
在论文中这一部分叫做激活模式(activation pattern)。
我们已经确定了这个点所在区域的半空间激活情况,但我们需要在第二个构造里通过这些激活模式找到对应的区域。
第二个构造
就像一开始提到的选择向量一样,我们在这里也需要一个选择矩阵。不妨设这个矩阵为,我们希望的结果是,对于,它能够将分区的超平面方程挑选出来。
我们现在考虑第个分区,它恰好可以由三个半空间交集而成。则我们可以考虑矩阵的第行为:
仅有第一、二、五列为,其余都为。
则有。
即的第行等于的第行乘上。
(我们还是举个例子)
最终结果是
假如我们的恰好处在第个分区,我们会发现,的第行恰好就是。由于我们的是声明所有分区的最小半空间集合,所以不可能出现同时有两行出现,否则就意味着我们的它同时处于两个不同的分区,又或者说,处在两个分区的交集上,这样它的半空间集合就不可能是最小的。(我们需要的是一种无交并的形式)。
第三个构造
我们在这一步会引入一个拓展实数,在数学上这样的拓展实数系代数性质很差,因为两个无穷大相除是没有结果的。但是我们在这里并不关心这件事,我们只引入两个基本的运算即可:
幸运的是在Python中包含这样的一个常量,用表示。
我们引入一个函数矩阵,不妨假定它一共有行。它的第行表示第个分区的对应的线性函数。则有:
根据我们上面提到的运算,只有第行才不为,而是对应的。
此时只需要经过一次即可将全部消除。
但实际上我们并不知道是否大于0。如果它小于0,那么经过以后也变成0了。因此我们构造的是:
这是一个行的向量,其中,要么是第行为,要么是第行为,已经无所谓了,我们只需要构造一个行向量,到列为,到列为,则有:
到这一步,我们就已经构造出来我们希望的东西了,只要我们找到,那么我们就可以利用刚才的构造,找到一个与原网络完全等价的一个浅层网络了。
(在论文里,作者对于第三个构造有一些数学上的考虑,以方便我们在后续的算法中找到神经网络的激活模式,但在推导的时候,这是trivial的)
对于,我们可以从前面发现他们是可以通过网络层的权重矩阵得到的。
对于,当我们找到所有的激活模式后,是可以通过以下的公式进行显式计算的,所以所有的任务就集中在我们应该找到网络的所有激活模式。至于具体的找到激活模式的算法在这里就不细讲了,因为涉及到另一篇很长的论文。